[허프만] 허프만 코딩 원리와 구현
안녕하세요.
오랜만에 포스팅을 합니다.
욕심쟁이 알고리즘 종류의 하나인 허프만 코딩에 대해 알아보겠습니다.

- 허프만 코딩
허프만 코딩은 문자의 빈도 또는 확률정보를 이용해 통계적 압축하는 방법인데요.
텍스트에서 문자가 출현하는 빈도수에 따라 다른 길이의 부호를 부여합니다.
예) 빈도가 높은 문자 : 짧은 코드, 빈도가 낮은 문자 : 긴 문자
또 접두부와 최적코드를 사용하고
이 두개의 뜻은 다음과 같습니다.
- 접두부(prefix code)
각 문자에 부여된 이진 코드가 다른 문자에 부여된 이진 코드의 접두부가 되지 않는 코드.
무슨말이냐 하면 겹치지 않도록 이진코드를 만드는 것이라고 할 수 있습니다.
예를 들어 a라는 문자에 101를 부여했을 때, b라는 문자에는 1, 10, 101 는 안된다는 걸 접두부라고 합니다.
| a -> 101 b -> 1, 10, 101은 부여할 수 없음. |
허프만 코딩은 접두부 코드가 되어야만 디코딩(인코딩 : 암호화, 디코딩 : 복호화)했을 때
문제가 발생하지 않기 때문에 꼭 적용되어야합니다.
- 최적코드
최적코드란 인코딩된 메시지의 길이가 가장 짧은 코드를 의미합니다.
이 2개를 바탕으로 인코딩 하는데 아래와 같습니다.
1. 주어진 텍스트에서 각 문자의 출현 빈도수를 계산합니다.
2. 각 문자의 빈도수를 이용하여 허프만트리를 생성하여 각 문자에 이진코드를 부여합니다.
3. 주어진 텍스트의 각 문자를 코드로 변환하여 압축된 텍스트를 생성합니다.
전체적인 인코딩 과정은 위와 같고 여기서 중요한 것은 허프만 트리를 생성해 이진코드를 부여하는 것입니다.
허프만 트리에 대한 것은 아래와 같습니다.
- 허프만 트리
상향식으로 만드는 이진트리로 욕심쟁이방법을 사용하고 전이진트리입니다.
전이진트리란?
리프노드를 제외한(단말노드) 나머지 모든 노드들은 자식을 2개씩 갖는 트리.
허프만 트리를 만드는 방법
| - 각 문자가 개별적인 트리인 상태에서 시작해서 빈도수가 작은 두 트리를 합쳐서 보다 큰 트리를 생성하는 과정을 반복 - 각 노드는 빈도수를 표시 - 좌우의 두 간선은 각각 0과 1로 써줌 - 합쳐지는 두 트리는 자식노드를 갖는 부모노드를 생성. - 부모노드의 빈도수는 두 자식 노드의 빈도수의 합 |
허프만 트리 예
역시 설명보다는 직접 해보는 편이 이해하기 편한데요.
한 번 다음 문자를 예로 들어보겠습니다.
"aaabrbacard"
1. 먼저 빈도수 별로 노드를 만들어 배치를 해줍니다.
(a가 문자에서 나타난 빈도수 : 5 노드 이런식으로)
2. 가장 작은 빈도수를 가지는 c, d가 있는데 를 합쳐서 부모노드를 만들고 값은 2입니다.
3. 합쳐진 c+d 부모노드의 왼쪽선은 0, 오른쪽 선은 1로 표시해줍니다.
4. 이런식으로 c와 d를 합친 부모노드와 b, r을 합친 부모노드를 합쳐 6의 값을 둔 부모노드를 만들고 왼쪽0, 오른쪽1.
5. 최종적으로 6을 가진 부모노드와 a와 합쳐 11의 값을 가진 노드가 생성됩니다.
여기서 중요한건 부모노드를 만들 때
왼쪽에는 0, 오른쪽에는 1을 두는것입니다.
이건 이진화 시킬 때 사용됩니다.
a의 선은 보면 0만 있는 걸 알 수 있습니다.
b를 찾아 내려가다보면 1, 0, 0이 되있습니다.(c : 110, d : 111, r : 101)
이진화 시킨 코드
| 문자 | 코드 |
| a | 0 |
| b | 100 |
| c | 110 |
| d | 111 |
| r | 101 |
이진화 시킨 것을 나타내면 아래와 같이 나타낼 수 있습니다.
"aaabrbacard" -> 00010010110001100101111(23비트)
위의 트리뿐 아니라 c와 d를 먼저 합친 수 r, b의 순서대로 합치는 방법도 있습니다.
이진화는 달라지겠지만 결론은 같은 23비트를 사용한다는 것입니다.
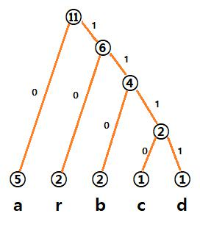
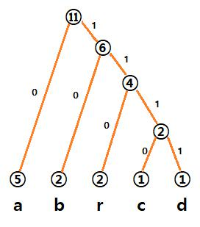
위 그래프는 이진화는 다르지만 결국 23비트 사용.....
- 성능 및 특징
- 허프만 트리를 만드는데 드는 시간 + 길이 m인 텍스트의 실제 인코딩 시간
O(nlogn) + O(m) = O(nlogn + m)
(logn에서 n은 문자집합의 크기)
- 각 문자의 빈도수를 모르는 경우 주어진 텍스트를 두 번 읽는다.
왜? 1. 각 문자의 빈도수를 계산할 때, 2. 텍스트를 읽으면서 실제 인코딩할 때-> 실용성 없다.
- 압축된 데이터를 디코딩 할때 정보가 필요하므로 압축률이 저하된다.
(문자의 빈도수, 트리 정보, 문자 집합 정보)-> 압축된 데이터의 정보를 제공할 헤더가 필요.
'Programming > 알고리즘' 카테고리의 다른 글
| [정렬] 선택정렬 (1) | 2018.08.03 |
|---|---|
| [정렬] 퀵정렬 (0) | 2018.06.28 |
| 열심히 해야지~ (0) | 2017.10.18 |
| [카르노 맵]카르노 맵의 정의 및 예제 (0) | 2017.08.29 |
| GrayCode 그레이 코드 변환 (0) | 2017.08.29 |











