[알고리즘] 브레젠험 알고리즘
선분그리기 알고리즘 중 대표적이고 정수계산이라 많이 쓰이는
브레젠헴, 브레젠험 알고리즘(Bresenham's algorithm)
오늘은 브레젠험 알고리즘의 원리와 구현방법을 포스팅하려합니다.
- 브레젠험 알고리즘의 사전적 의미
Bresenham의 선 알고리즘 은 두 점 사이 의 직선에 가까운 근사를 형성하기 위해 선택해야하는 n 차원 래스터 의 점을 결정하는 알고리즘 입니다. 비트 맵 이미지 (예 : 컴퓨터 화면 )에 선 프리미티브 를 그릴 때 주로 사용되며, 정수 추가, 빼기 및 비트 쉬프트 만 사용하므로 표준 컴퓨터 아키텍처 에서 매우 저렴한 작업입니다. 증분 오류 알고리즘 입니다. 컴퓨터 그래픽 분야에서 개발 된 최초의 알고리즘 중 하나입니다. 원 알고리즘을 확장하면 원 그리기에 사용될 수 있습니다. Wu의 알고리즘과 같은 알고리즘 은 안티 앨리어싱 을 지원할 수 있기 때문에 최신 컴퓨터 그래픽에서 자주 사용되지만 Bresenham의 회선 알고리즘의 속도와 단순성은 여전히 중요하다는 것을 의미합니다. 알고리즘은 플로터 및 최신 그래픽 카드 의 그래픽 칩 과 같은 하드웨어에서 사용됩니다. 또한 많은 소프트웨어 그래픽 라이브러리 에서 찾을 수 있습니다. 이 알고리즘은 매우 간단하기 때문에 현대그래픽 카드 의 펌웨어 또는 그래픽 하드웨어 에서 구현되는 경우가 많습니다.
"Bresenham"이라는 레이블은 오늘날 Bresenham의 원래 알고리즘을 확장하거나 수정하는 알고리즘 계열에 사용됩니다.
????? 위키피디아에 엄청 잘 나와있네요. 포스팅 안해도 될만큼
근데 혹시 또 모르니 저도 알고있는만큼 쉽게 포스팅하겠습니다.
- 직선의 방정식
넵 또 나왔습니다. 직선의 방정식
브레젠험을 정확히 이해하기 위해서는 직선의 방정식도 정확히 알아야됩니다.
직선의 방정식은 원리를 정확히 반복이해해서
y = mx + b
공식이 딱 나오는게 좋습니다.
직선의 방정식이 게임프로그래밍에서 꼭 쓰이는 부분이 있는데 바로
내가 찍은 점이 직선 위에 있느냐, 아래 있느냐, 아니면 직선상에 존재하느냐입니다.
만약 쿼터뷰(마름모타일)게임에서는 캐릭터나 오브젝트가 서있는 위치를 판별할 때
마름모의 각 선분(직선)으로 판단하기 때문입니다.
만약
의 직선의 방정식에서
기울기(m) : 1
y절편(b) : 0
이라고 가정해볼때 (계산하기 쉽게 하기 위해)
라는 알기 쉬운 직선의 방정식입니다.
(x = 1일때 y = 1이고 x = 2일때 y = 2.....이런 좌표를 지나가는 직선)
참고로 기울기는
입니다.
위 직선에서 캐릭터가 서 있는 위치를 빨간점(x = 2, y = 5)과 노란점(x = 3, y = 1)이라고 가정합니다.
(이번 포스팅에 쓴 좌표계는 위의 좌표그림과 약간 다른데요~ 네모 한 칸당 좌표 점입니다.)
만약 위에 왼쪽 그림처럼 빨간점(2, 5)좌표를 직선의 방정식(y = x)에 대입해보면
y = 5, x = 2가 되서 5 = 2가 됩니다.
같지 않으니까 5 > 2이런식으로 나타낼 수 있습니다.
(2, 5)좌표는 딱 봐도 직선보다 위에 있죠? 그러니
현재 좌표가 직선보다 위에 있을 때 y > x
라고 나타낼 수 있습니다.
반대로 오른쪽 그림처럼 노란점(3, 1)일 경우는 1 = 3, 1 < 3입니다.
현재 좌표가 직선보다 아래에 있을 때 y < x
마지막으로
현재 좌표가 직선상에 있으면 y = x입니다.
이건 쉽게 나타낸 직선의 방정식으로 해본건데
기울기의 값이 2거나 y절편의 값이 있을때도 똑같은 결과가 나옵니다.
우리는 눈으로 보면 캐릭터나 좌표가 직선 위에 있는지 아래 있는지 바로 알 수 있지만
컴퓨터는 위와 같은 판별식으로 판단해야됩니다.
여튼 직선의 방정식에는 이런 성질이 있다는 걸 알면
브레젠험 알고리즘을 더 이해하기 쉬울것입니다.
- 브레젠험 알고리즘 원리
실수 연산이 필요 없고 정수 연산만으로 처리되는 속도가 매우 빠른 래스터 방식 컴퓨터 그래픽에서 선을 긋는 알고리즘.
이 방법은 가로나 세로의 어느 한쪽 좌표를 시작점으로 하여 종료점까지 1씩 가산하여 좌표를
증가시킬 것인가 또는 그대로 유지할 것인가를 판단한다.
[네이버 지식백과] 브레젠험의 알고리즘 [Bresenham's algorithm]
(컴퓨터인터넷IT용어대사전, 2011. 1. 20., 일진사)
라고 설명이 나와있는데요.
전에 DDA알고리즘은 실수를 반올림을 하는 연산이 있어 속도저하가 있을 수 있다했습니다~
DDA알고리즘 포스팅
https://playground10.tistory.com/58?category=253099
그럼 이제부터 제일 중요한
브레젠험알고리즘의 원리 및 정수형 판별식을 구하는 원리입니다.
1. 기울기가 0과 1사이인 직선을 가정해줍니다.
현재좌표를 k번째라고 하고 x좌표는 Xk, Y좌표는 Yk라고 가정하겠습니다.
2. 현재 좌표에서 다음 찍어야할 좌표값을 구해야되는데
x는항상 1만큼 증가하고,
y는Yk, Yk+1둘 중 하나를 선택합니다.(둘 중 어떤걸 선택하는가 기준은 중단점Mk + 1로 판별합니다.)
다음 y좌표 선택 판단기준 -> 중단점Mk+1 (매우 중요)
3. 만약 중단점(Mk+1)이우리가 임의로 설정한직선 위에 위치 -> y값은 그대로 Yk 선택
반대로 중단점(Mk+1)이 직선의 아래에 위치 -> y값은 1증가해서 Yk+1 선택
4. 여기서 중요한건 중단점 Mk+1이 직선 위에 있냐 아래있냐로 다음 점을 판단한다
는것인데 그 판별식을 구해줘야됩니다.
구하는 방법은 다음과 같습니다.
판별식 구하는 방법
 ① 위에 입력받은 좌표 2개 (Xl, Yl), (Xr, Yr) 로 분홍색 직선 하나(Xl, Yl) - (Xr, Yr)를 만들어줍니다. ② W와 H를 구해줍니다. W = Xr - Xl H = Yr - Yl  ⑥ 이걸 부등호를 이용해 식을 나타내보면 위에 직선의 방정식에서 나왔듯이  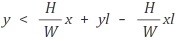 이렇게 되겠죠? ⑦ y값을 넘겨서 한쪽을 0으로 나타내보면   이렇게 되고 아래와 같이 위치를 바꿔서 나타내주겠습니다.  ⑧ 이 식에 W를 곱해줍니다.(분모를 없애기 위해), 참고로 이걸 하는 과정은 정수의 식을 만들어주기 위해서입니다.  ⑨ 8번에서 나온 식에 2를 곱해줍니다.  이런식이 나오는데 이 식은 간단히 나타내주면  이제 이 식으로 판별을 해줍니다. ⑩ 위 식은 아래 두 가지 경우로 구별됩니다. -2W( y - yl ) + 2H ( x - xl ) < 0 // 직선보다 위에 있을때 -2W( y - yl ) + 2H ( x - xl ) > 0 // 직선보다 아래 있을때 자 이제 판별식 구하는 공식이 끝났습니다. 다시 브레젠험 알고리즘 원리에 대해 마저 알아보겠습니다. |
5. 위에서 구한 판별식으로 중단점의 위치를 판단해
다음 점 (Xk+1, Yk+1)의 좌표를 각각 구해줍니다.
5_1. 중단점이 어디 있을지 판단.
① 만약에 중단점(빨간원)이 직선보다 위에 있을때
-2W( y - yl ) + 2H ( x - xl ) < 0
위 그림과 같이 되는데 이 때 다음 좌표는 (Xk+1, Yk) 입니다. (초록색테두리)
② 반대로 중단점(빨간원)이 직선 아래 있을 때
-2W( y - yl ) + 2H ( x - xl ) > 0
다음 좌표는 (Xk+1, Yk+1)
정리하자면 판별식
F(Mk+1) =
-2W( y - yl ) + 2H ( x - xl ) < 0
→ Mk+1이 직선의 위에 있음 → (xk+1, yk)
-2W( y - yl ) + 2H ( x - xl ) > 0
→ Mk+1이 직선의 아래에 있음 → (xk+1, yk+1)
6. ( xk + 1 , yk + 1 ) 을 결정하기 위한 판별식을 구해줍니다.
중단점 Mk+1 = ( xk + 1, yk + 0.5 )가 됩니다.
(중간에 있으니 ½인 0.5를 y값에 더한 값이 중단점입니다.)
이걸 5번에서 구한 식에 대입해주면
F(Mk+1) = -2W( yk + 0.5 - yl ) + 2H ( xk + 1 - xl )
이 됩니다.
7. 그 다음 중담점인 (xk+2, yk+2) 을 결정하기 위한 판별식을 구해줍니다.
7_1. 첫번째 F(Mk+1) < 0 인 경우
( 중단점이 직선 위에 있어서 다음점 y값이 그대로였던 경우 )
위 그림에서 보면 Mk+2(두번째 중단점)는
Xk + 2와 Yk + 0.5임을 알 수 있습니다.


이였지요?
위에 F(Mk+2)와 매우 비슷합니다.
식을 비교해보면 앞부분은 똑같고(-2W(y어쩌고))
+ 2H(x어쩌고 하는 부분)을 풀어주면 딱 2H 만큼 더해주면 되네요.

최종적으로 이런식으로 나타낼 수 있습니다.
7_2. 두번째 F(Mk+1) > 0 인 경우
( 중단점이 직선 아래에 있어서 다음점 y값이 1올라간 경우 )
초록색네모점이였으니 그 다음 중단점의 위치는 아래와 같이 구합니다.

풀어서 비교해 주면 아래와 같습니다.
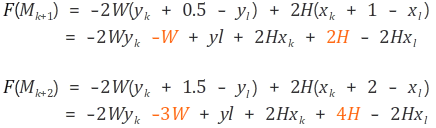
바뀐 부분은 -2W와 2H 입니다.

최종적으로 이런식으로 나타낼 수 있습니다.
8. 판별식의 초깃값 F(M1)을 구해줍니다.

9. 마지막으로 다음 픽셀 위치의 결정 및 판별식 갱신식만 구해주면
브레젠헴 알고리즘을 구현할 준비는 끝입니다.
9_1. F < 0 인 경우
- 위 5번에서 나왔듯이 (Xk+1, Yk)위치에 점을 그림.

- 판별식은 기존판별식에 2H를 더해줌.
- 2H를 더해주는 걸 모르겠으면 7_1번을 다시 보면 됩니다.
9_1. F > 0 인 경우
- 위 5번에서 나왔듯이 (Xk+1, Yk+1)위치에 점을 그림.

- 판별식은 기존판별식에 2(H-W)를 더해줌.
- 2(H-W)를 더해주는 걸 모르겠으면 7_2번을 다시 보면 됩니다.
휴 너무 길었죠? 하지만 천천히 그림도 그려보고 적어가면서 수식을 풀어보면 더 알기 쉬워요.
- 브레젠험 알고리즘 적용
이제 위에 구한 판별식과 초깃값으로 브레젠헴알고리즘을 적용해 직선을 그려볼건데요.
아마 이 단계를 하면 감도 잡히고 이해가 잘 될겁니다.
| 1. 먼저 직선의 시작점과 끝점을 입력받습니다.(예: (1, 1) - (7, 5) ) 2. 입력받은 시작점으로 W와 H를 구해 2H-W에 대입해 처음 초기값F을 구해줍니다. 3. F의 값이 0보다 크냐 작냐에 따라 판별식 F을 통해 다음 점을 찍어줍니다. 4. 기존 F에 각각 다른 공식을 F에 더해준다. 5. 새로 나온 F로 직선위냐 아래냐인 판별식을 통해 점을 찍어준다.(3번과 같음) 이런식으로 반복해 끝점까지 직선을 만들어주면 됩니다. |
여기까지는 간단히 설명한 것이였고 아래 직접 해본것입니다.
1. 먼저 초깃값및 판별식을 계산해줍니다.(정수화)
입력받은 점 가로, 세로 각 케이스별 판별식(0보다 작을 때, 0보다 클때) |
2. 조건에 따라 판별식 공식을 구해줍니다.
 판별식(중단점)이 0보다 작으면 다음 y값은 그대로이고 판별식은 기존판별식에 8을 더해주고요. 0보다 크거나 작으면 y값은 1증가 판별식에 4를 빼줍니다. |
3. F에 따라 다음 좌표를 찍어주고 판별식F를 갱신해줍니다.
| 0 | 2 (처음 초기값은 2) | ( 2 , 2 ) // F가 0보다 크므로 y값 증가 |
| 1 | -2 (2 - 4 = -2, 기존F가 2였으므로 0보다 큰 공식으로 구해줌.) |
( 3 , 2 ) // F가 0보다 작으므로 y값 그대로 |
| 2 | 6 (-2 + 8 = -6, 기존F가 -2였으므로 0보다 작은 공식으로 구해줌.) |
( 4 , 3 ) // F가 0보다 크므로 y값 증가 |
| 3 | 2 (6 - 4 = 2) | ( 5 , 4 ) |
| 4 | -2 (2 - 4 = -2) | ( 6 , 4 ) |
| 5 | 6 | ( 7 , 5 ) |
브레젠험 알고리즘으로 직선을 찍은 모습.
- 브레젠험 알고리즘 구현
bool bresenham(int _startX, int _startY, int _FinishX, int _FinishY)
{
// H/W는(기울기)0과 1사이로 가정
// 처음 찍을 점은 시작점으로 한다.
int x = _startX;
int y = _startY;
// W와 H를 구해줌.
int W = _FinishX - _startX;
int H = _FinishY - _startY;
// 초기값
int F = 2 * H - W;
// 각 판별식공식
int dF1 = 2 * H;
int dF2 = 2 * (H-W);
for( x = _startX; x <= _FinishX; ++x )
{
// 첫 시작점 그리기
setPixel(x, y);
// 중단점이 0보다 작으면 그에 맞는 공식으로 판별식 갱신, y값은 그대로
if( F < 0 )
{
F += dF1;
}
else // 중단점이 0보다 크거나 같으면
// 그에 맞는 공식으로 판별식 갱신, y값은 증가
{
++y;
F += dF2;
}
}
return true;
}
감사합니다.
'Programming > 알고리즘' 카테고리의 다른 글
| [허프만] 허프만 코딩 원리와 구현 (0) | 2018.04.27 |
|---|---|
| 열심히 해야지~ (0) | 2017.10.18 |
| [카르노 맵]카르노 맵의 정의 및 예제 (0) | 2017.08.29 |
| GrayCode 그레이 코드 변환 (0) | 2017.08.29 |
| [알고리즘] DDA알고리즘 (1) | 2017.06.19 |


























